Phy 131 homework, continued. (Reading refers to Serway & Jewett’s Physics for Scientists & Engineers with Modern Physics, 10^th ed.)

Sec. 5: Work and Energy

Read: sec. 7.2-7.7, 8.2-8.4 (skip stuff about springs.)

Quiz A. A pendulum consists of a 5.00 kg mass on a light string 2.00 m long. The mass is given an initial speed of 4.00 m/s at its lowest position. When the string makes an angle of 37° with the vertical, find:

a. The change in the potential energy of the mass.

b. The speed of the mass.

ans. 19.7 J, 2.85 m/s

B. 1. (1 point) When a particle revolves around a circle, a force acts on it directed toward the center of the circle. Why is it that this force does no work on the particle?

2. (2 points) Including air friction, consider a ball thrown straight up which then returns to the thrower's hand. State when each of the following is greatest, or that it remains constant:

i. Potential energy, U_g.

ii. Total mechanical energy, E.

3 (7) A 3.00 kg mass has an initial velocity of = (6.00 – 2.00) m/s. (a) What is its kinetic energy at this time? (b) Find the total work done on the object if its velocity changes to (8.00 + 4.00) m/s. (Hint: Remember that v² = .)

ans: 60.0 J, 60.0 J

C. 1. (2 points; .4 each) What is the value of each product?

× = _____, × = _____, × = _____, × = _____, × = _____

2. (1 point) A stunt man hangs by a rope from a large balloon. As the balloon moves 100 m, 50 000 J of work is done on the man by the 500 N tension in the rope. Did the balloon move horizontally, vertically, or could it be either?

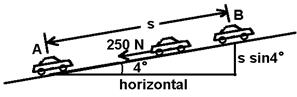3. (7) A 1200 kg car with 540,000 J of kinetic energy runs out of gas at point A. It then coasts up a hill as shown, while experiencing a drag force of 250 N. What is the distance, s, that it coasts before coming to rest at point B?

ans: 505 m

D. 1. (1 point) Another student tells you they have calculated the work done on an object to be

3.50– 1.80 J. Something should look wrong to you. What is it?

2. (9) A 15 kg block is dragged over a horizontal surface by a 70 N force acting at an angle of 20° above the horizontal. The block is displaced 5.0 m and the coefficient of kinetic friction is 0.3. Find (a) the work done by the 70 N force, and (b) the work done by the force of friction.

ans. 329 J, –185 J

E. 1. (1 point) When nonconservative forces act on a system, does the total mechanical energy remain constant?

2. (9) A 250 gram glider slides horizontally along the x axis on a frictionless air track. A string tied to the glider is pulled with a constant force of F = .700 + .400 N. After being displaced 3.00 m from rest, (a) how much work has been done on the glider? (b) what is its speed?

ans: 2.10 J, 4.10 m/s

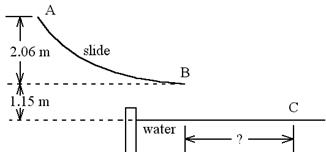F. A slide is attached to a swimming pool as shown. A 22 kg child starts at rest at point A, then is launched horizontally from point B.

a. If 35 J is lost to friction along the slide, what is her speed at B?

b. How much time is she in the air?

c. How far from the point directly under point B does she hit the water?

ans: 6.10 m/s, .484 s, 2.96 m

Sec. 6: Power / Newton's Third Law and Momentum:

Read: sec. 5.6, 8.5, 9.1 - 9.5

A. 1. (2 points) A ball is dropped. (a) What force acts on it while it is falling? (Neglect air resistance.) (b) Identify the reaction force.

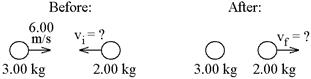2. (8) A 3.00 kg object and a 2.00 kg object have a perfectly elastic head-on collision as shown. (a) How fast must the 2 kg hit the 3 kg to make the 3 kg stop? (b) How fast is it moving after the collision?

ans: 1.50 m/s, 7.50 m/s

B. 1. (4 pts) A 1500 kg car accelerates uniformly from rest to 10 m/s in 3.0 s. Find (a) the work done on the car in this time, (b) the average power delivered by the engine in the first 3.0 s.

ans: 7.5 x 10⁴ J, 2.5 x 10⁴ W (or 33.5 hp)

2. (6) A .150 kg baseball is thrown at a speed of 40.0 m/s. It is hit straight back at the pitcher with a speed of 50.0 m/s. (a) What is the impulse delivered to the baseball? (b) Find the average force exerted by the bat on the ball if the two are in contact for 2.00 x 10^-3 s.

ans: 13.5 kg×m/s, 6.75 x 10³ N, both toward the pitcher

C. 1. (2 points) Newton's third law states that every force has a reaction force which is equal in magnitude and opposite in direction. If this is the case, how can the net force on an object ever add up to anything other than zero?

2. (8) An unstable nucleus of mass 17.0 x 10^-27 kg, initially at rest at the origin, disintegrates into three particles. One of the particles, mass = 5.00 x 10^-27 kg, moves up the y axis with a velocity of 6.00 x 10⁶ m/s. Another, of mass 8.40 x 10^-27 kg, moves along the positive x axis at 4.00 x 10⁶ m/s. Find the third particle's velocity vector.

ans: (–9.33 – 8.33) x 10⁶ m/s

D. A 10.0 kg object moving to the right with a speed of 3.00 m/s makes an elastic head on collision with a 20.0 kg object initially at rest. Find the final velocity of each.

ans.: –1.00 m/s, 2.00 m/s

E. A 90 kg fullback running east with a speed of 5.00 m/s is tackled by a 95 kg opponent running north with a speed of 3.00 m/s. If the collision is perfectly inelastic, calculate the speed and direction of the players just after the tackle.

ans: 2.88 m/s at 32.4° north of east

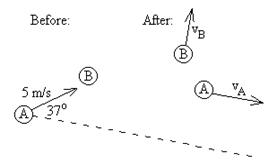
F. Two frictionless pucks have a somewhat inelastic, glancing collision. Puck B is 1.25 times the mass of puck A. Initially, B is at rest and A is moving at 5.00 m/s at an angle of 37.0° with its final direction of motion. After the collision, the pucks are moving in perpendicular directions. (a) What is v_A? (b) What is v_B? ans: A: 3.99 m/s, B: 2.41 m/s

Sec. 7: Rotation

Read: Ch. 10, sec. 1 – 5 & 7

A. 1. (2 points) A wheel is rotating about a fixed axis. Do all points on the wheel have the same (a) angular velocity? (b) linear velocity?

2. (8) The angle which a certain rotating object has turned through is given by θ = 5t³ – 30t + 10, where t is in seconds and θ is in radians.

a. Find its angular velocity at t = .800 s.

b. Find its angular acceleration t = .800 s.

c. At what time does the object stop turning clockwise and start turning counterclockwise?

ans: –20.4 rad/s, 24.0 rad/s², 1.41 sec.

B. 1. (2 points) An old style record player turntable rotates at a constant 45 rev/min.

a. What is its angular speed in radians per second?

b. What is its angular acceleration?

2. (8) A 25.0 cm radius wheel has a 10.0 cm radius axle. A string wound around the wheel pulls with 90.0 N and a string around the axle pulls with 120 N. The box which makes the 90.0 N force accelerates downward at a = 5.10 m/s². What is the moment of inertia of the wheel and axle?

ans: .515 kg×m²

C. 1. (1 point) If you see an object rotating, is there necessarily a net torque acting on it?

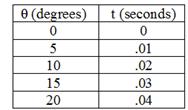
2. (1) A wheel’s position is measured every .0100 s, giving the data shown in the table. What is its angular acceleration in degrees/s²?

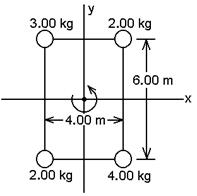
3. (8) The four particles shown are connected by rigid rods of negligible mass. They rotate about the z axis, which passes through the page at the center of the rectangle, with an angular speed of 6.00 rad/s. Find the system's

a. moment of inertia about the z axis, and

b. rotational kinetic energy.

ans: 143 kg×m², 2.57 kJ

D. A long uniform rod of length L and mass M rotates in a vertical plane about a frictionless pivot at one end. It is released from rest in a vertical position. At the instant it passes through the horizontal, find (a) its angular speed, and (b) the magnitude of its angular acceleration.

ans: ω = , α = 3g/(2L)

E. 1. (1.5 points) Why does a tightrope walker carry a long pole for balance instead of a bowling ball of the same mass?

2. (8.5) A long uniform rod of length L and mass M rotates in a vertical plane about a frictionless pivot at one end, as shown above. It is released from rest in a vertical position. It can be shown that as it passes through the horizontal, its angular speed is ω = and the magnitude of its angular acceleration is α = 3g/(2L). Find the x and y components of the acceleration of its center of mass.

ans: = – (3/2)g – (3/4)g

F. A wheel 1.00 m in diameter rotates on a fixed, frictionless axle. Its moment of inertia about this axis is 5.00 kg×m². A constant tension of 20.0 N is maintained on a rope wrapped around the rim of the wheel. If the wheel starts from rest at t = 0, find

a. the wheel's angular acceleration, (ans: 2.00 rad/s²)

b. the wheel's angular speed at t = 3.00 s, (ans: 6.00 rad/s)

c. the length of rope unwound in the first 3.00 s (ans: 4.50 m)

Sec. 8: Torque & Statics

Read: ch. 11, sec. 1; ch. 12 all except sec. 2 & 4

A. 1. (1 point) Can a body be in equilibrium if it is in motion?

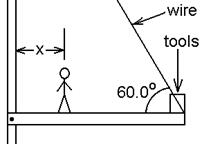
2. (9) A construction worker weighing 700 N walks out on a beam in an attempt to retrieve a box of tools at the end. The beam is uniform, weighs 200 N, and is 6.00 m long. The tools weigh 80.0 N. When the worker is at x = 1.00 m, find the tension in the wire, and the components of the force exerted by the wall on the left end of the beam.

ans: T = 343 N, H = 171 N, V = 683 N,

B. 1. (2 points) What is the value of each product? x=____, x=____, x=____, x=____, x=____, x=____

2. (8) A construction worker weighing 700 N walks out on a beam in an attempt to retrieve a box of tools at the end, as shown above. The beam is uniform, weighs 200 N, and is 6.00 m long. The tools weigh 80.0 N. If the wire can withstand a maximum tension of 900 N, what is the maximum distance, x, the worker can walk before the wire breaks?

ans: x = 5.14 m

C. A bridge of length 50.0 m and mass 8.00 x 10⁴ kg is supported only at its ends, points A and B. A truck of mass 3.00 x 10⁴ kg is located 15.0 m from end A. What are the forces on the bridge at each point of support?

ans: F_A = 5.98 x 10⁵ N, F_B = 4.80 x 10⁵ N

D. A 15.0 m uniform ladder weighing 500 N rests against a frictionless wall. The ladder makes a 60.0° angle with the horizontal. Find the horizontal and vertical forces that the ground exerts on the base of the ladder when an 800 N firefighter is 4.00 m from the bottom.

ans: H = 268 N, V = 1300 N

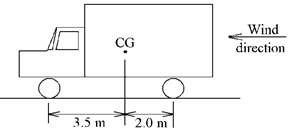
E. The truck plus contents weighs 50.0 kN. The wind’s force is a horizontal 1.20 kN effectively acting at a point 1.70 m above the ground. The front wheels are free to roll, so there is only a vertical force pushing up on them. Because the parking brake is on, the ground exerts both horizontal and vertical components on the rear wheels. Find (a) the total vertical force on the front wheels from the ground, (b) the total vertical force on the rear wheels from the ground, and (c) the total horizontal force on the rear wheels from the ground.

ans: 18.6 kN, 31.4 kN, 1.20 kN

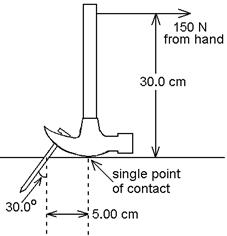
F. The figure shows a stationary claw hammer being used to try and pull a nail. The force on the hammer from the nail is parallel to the nail, and the force from the hand is horizontal. If the hand exerts 150 N, what is (a) the magnitude of the force from the nail, and (b) the force exerted by the surface on the point of contact with the hammer head?

ans: 1.04 kN, 370 + 900 N

Sec. 9: More Rotation

Read: Ch. 10 sec. 8 & 9; Ch. 11 sec. 2 - 4.

A. During a supernova, the core of the exploding star collapses, sometimes becoming a very compact object called a neutron star. Assume that the net force on each particle of the imploding core, as it falls inward, is directly toward the star’s center. If the original core had a mass of 5.00 x 10³⁰ kg, a radius of 10 000 km and spun at a rate of one revolution per day, and if the resulting neutron star has the same mass and a 10 km radius, what are its final (a) angular momentum, (b) rotational kinetic energy and (c) angular velocity?

ans: 1.45 x 10⁴⁰ kg·m²/s, 5.29 x 10⁴¹ J, 72.7 rad/s

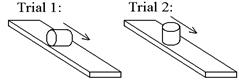B. 1. (2 points) Compressed air blows out of a ramp's surface, similar to our air tracks. With the air off, a solid plastic cylinder is rolled down the ramp without slipping. Then with the air on, it is slid down the ramp on its end, without rolling. No significant energy is lost to friction in either case, and the center of mass drops the same distance in both cases. In which trial does it get to the bottom quicker, or is it the same? (Considering conservation of energy might be helpful.)

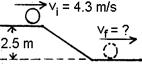
2. (8) A solid sphere rolls down a ramp without slipping, as shown. What is its final speed if there are no losses to friction?

ans: 7.31 m/s

C. C. A basketball (thin spherical shell) with a radius of 12.0 cm rolls past point A at 3.50 m/s, then rolls up a curved ramp and shoots straight up from the top. It rolls without slipping until it shoots off the ramp at point B, and negligible energy is lost to friction. C is the highest point it reaches.

a. What is its speed at point B?

b. What is its angular speed at point B?

c. What is its speed at point C?

d. What is its angular speed at point C?

ans: 2.00 m/s, 16.7 rad/s, 0, 16.7 rad/s

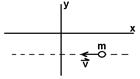
D. 1. (2 points) What is the direction of this particle's angular momentum vector?

2. (8) A playground merry-go-round of radius R = 2.00 m has a moment of inertia of I = 250 kg×m² and is rotating at 10 rev/min about a frictionless vertical axis. A 25 kg child hops on, moving straight toward the axis, and landing at the merry-go-round's outer edge. What is its new angular speed?

ans: 7.14 rpm

E. 1. (2 points) Three objects of uniform density - a solid sphere, a solid cylinder and a thin hollow cylinder - are placed at the top of an incline. If they all are released from rest at the same elevation and roll without slipping, which object reaches the bottom first? Which reaches it last?

2. (8) A woman on a lawn tractor is pulling a cylindrical 50.0 kg roller over level ground. The roller passes point A at 1.75 m/s. If the net work done on the roller between points A and B is 190 J, what is its speed (in m/s) at point B?

ans: 2.85 m/s

F. A particle of mass 10.0 g and initial speed 5.00 m/s collides with and sticks to the edge of a uniform solid sphere of mass 1.00 kg and radius 20.0 cm, as shown. If the sphere is initially at rest and is pivoted about a frictionless axle through its center which is perpendicular to the page, find

a. the angular velocity of the system after the collision,

b. how much energy was lost in the collision.

ans: .610 rad/s, .122 J

Sec. 10: Springs and Vibration:

Read: Those parts of ch. 7 & 8 which are about springs; ch. 15 up to the heading "The physical pendulum" on P.402.

A. The motion of a piston in an engine is simple harmonic. If the displacement of a certain piston varies according to

x = (5.00 cm)cos(2.00t + π/6)

where x is in cm, and t is in seconds, find

a. the piston's displacement at t = 0,

b. its velocity at t = 0,

c. its acceleration at t = 0,

d. the period of its motion, and

e. the amplitude of its motion.

ans: 4.33 cm, –5.00 cm/s, –17.3 cm/s², 3.14 s, 5.00 cm

B. 1. (1 point) A spring stretches two inches when a certain weight is hung from it. The spring is then cut in half; the same weight stretches either half one inch. The spring constant of either piece is __________ the original spring's. (more than? less than? the same as?)

2. (9) A block of mass .250 kg is placed on top of a vertical spring of constant k = 5000 N/m and pushed downward, compressing the spring .100 m. After the block is released, it travels upward and then leaves the spring. To what maximum height above the point where your hand released it does it rise?

ans: 10.2 m

C. Approximating small changes with differentials: A simple pendulum has a length of 2.50 m. Determine the change in its period if it is taken from a point where g = 9.80 m/s² to an elevation where the free-fall acceleration is 9.79 m/s², as follows: (a) Do this by calculating the differential of the formula for T, then filling numbers into the result. (b) Find exactly what the change really is by calculating T at each location and subtracting.

ans to both a & b: increases by .00162 s

D. 1. (3 points) Can the following quantities be in the same direction for a simple harmonic oscillator?

a. Displacement and velocity? ____________

b. Velocity and acceleration? ____________

c. Displacement and acceleration? ____________

2. (7) A 130 gram mass, attached to a spring, is moving on a frictionless horizontal surface. It passes through equilibrium at 5.00 m/s. If the spring has a stiffness of k = 67.0 N/m, what is its speed when the mass is 15.0 cm from equilibrium?

ans: 3.66 m/s

E. 1. (1 point) If a mass - spring system is hung vertically and set into oscillation, why does the motion eventually stop?

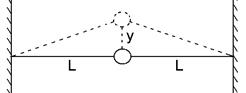
2. (9) A frictionless puck of mass m is connected to two rubber bands of length L, each under tension T, as shown. This is on a smooth, horizontal sheet of ice. The puck is displaced a small distance y perpendicular to the rubber bands. When released, it vibrates along the y axis. Assuming that the tension does not change,

(a) show that the restoring force is – (2T / L)y and

(b) find the expression for how the angular frequency depends on m, L and T.

ans: ω =

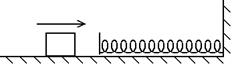F.

A 3.0 kg block, sliding on a horizontal surface with a coefficient of kinetic friction of .30, collides with a horizontal massless spring with a force constant of 30 N/m. Its speed is 1.5 m/s when it first touches the spring. How far will it compress the spring before stopping momentarily?

ans: 26.4 cm

Sec. 11: Waves

Read: Ch. 16: Sec. 1 – 3, 8 & 9, except shock waves.

Ch. 33: sec 7

A. 1. (2 points) Name four different kinds of electromagnetic waves (not necessarily in order).

2. (8) A sinusoidal wave train is described by the equation

y = (.250 m)sin[(.300 m^-1)x – (40.0 s^-1)t)]

Find this wave's (a) amplitude, (b) angular frequency, (c) wave number, (d) wavelength, (e) wave speed, (f) direction of motion (right or left) and (g) displacement at x = 3.20 m when t = .190 s.

ans: .250 m, 40.0 rad/s, .300 rad/m, 20.9 m, 133 m/s, right, –.0873 m

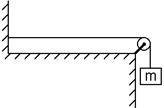B. 1. (2 points) How do transverse waves differ from longitudinal waves?

2. (8) A sinusoidal wave in the rope shown is described by the wave function y = (.200)sin(.750πx – 18.0πt) where x and y are in meters and t is in seconds. The rope has a linear mass density of .250 kg/m. What is the value of the suspended mass, which is providing the tension in the rope?

ans: 14.7 kg

C. 1. (4 points) You are standing by the side of a road, just about directly in front of an approaching car which is blowing its horn. Point A is 1000 ft in front of you, point B is 500 ft in front of you, and point C is 500 ft behind you. If the car maintains a constant velocity,

a. When the car is at A, how does the pitch you hear compare to the pitch heard by the driver?

b. When the car is at B, how does the pitch you hear compare to the pitch you heard when it was at A?

c. When the car is at C, how does the pitch you hear compare to the pitch you heard when it was at B?

d. When the car is at C, how does the pitch you hear compare to the pitch heard by the driver?

2. (6) A sinusoidal wave is traveling along a rope. The oscillator which generates the wave completes 40.0 vibrations in 30.0 seconds. Also, a given maximum travels 425 cm along the rope in 10.0 seconds. What is the wavelength?

ans: .319 m

D. 1. (2.5 points) Name the colors of the visible spectrum in order. Which color has the highest frequency? The longest wavelength?

2. (7.5) A train passes a platform at 40.0 m/s, with its horn blowing. The engineer hears the horn's frequency to be 320 Hz. What change in frequency is observed by a person on the platform as the train passes?

ans: 75.7 Hz drop

E. The sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be 100 dB?

ans: 30.0 m

F. With 100 people talking in a restaurant, the sound level is 80.0 dB. What is the average sound level later, with only five people left? Assume that the people are the only significant source of sound, the conversations never die down and each person is equally loud.

ans: 67.0 dB

Sec. 12 - Gravitation/ Temperature & The Ideal Gas Law

Read: Ch. 13, sec. 1, 2 & 4; those parts of sec. 18.2 & 18.3 which define temperature scales;

sec. 18.5

A. You are an astronaut visiting a spherical asteroid (a very small planet). Walking directly away from your ship in a straight line, you find yourself back at it after walking 6.3 km. Releasing a hammer from a height of 2.0 m, you observe that it reaches the ground after 69 seconds. Find the planet's mass. ans: 1.27 x 10¹³ kg

B. 1. (2 points) Two cylinders of the same kind of gas are at the same temperature and hold the same number of moles of gas. If the volume of cylinder A is three times the volume of cylinder B, how does the pressure in A compare to the pressure in B?

2. (8) A vacuum system attains a pressure of 1.00 x 10^-9 Pa. Calculate the number of molecules in a 1.00 m³ vessel at this pressure if the temperature is 27.0°C.

ans: 2.41 x 10¹¹

C. You check the pressure in one of your tires, and the gauge reads 31.0 lb/in². Having just been driven, the tire is at 45.0°C.

a. As the car sits in the parking lot, the tire cools to 11.0°C. If you check the pressure after it cools, what does the gauge read?

b. After that, a mechanic removes the tire from the rim, which lets the air out. How much volume will the air from the tire occupy after being released into the atmosphere? The tire's volume is 20.0 liters, and the temperature of the atmosphere is 11.0°C.

ans: 26.1 lb/in², 55.5 liters

D. In an effort to explain the timing of large meteor collisions with the earth, a distant, dim companion star was once suggested for our sun. If this star (which they called Nemesis) had an orbital period of 3.0 x 10⁷ years, and a mass of .20M_sun, determine its average distance from the sun. M_sun = 2.0 x 10³⁰ kg.

ans: 1.54 x 10¹⁶ m

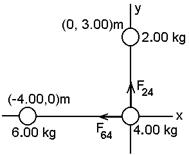
E. Three uniform spheres are placed at the corners of a right triangle, as shown. Calculate the magnitude and direction of the resultant gravitational force on the 4.00 kg mass, assuming that the rest of the Universe is far away enough to ignore. (F₆₄ means the force the 6 kg makes on the 4 kg and F₂₄ means the force the 2 kg makes on the 4 kg.)

ans: 116 pN at 149°

F. 1. (5 points) A satellite is put into an orbit with the following parameters: perigee, 459 km; apogee, 2289 km (both distances above Earth's surface); and period, 6762 s. Find the ratio v_p/v_a of the speed at perigee to the speed at apogee.

ans: 1.27

2. (5) Io, a satellite of Jupiter, has an orbital period of 1.53 x 10⁵ s and an orbital radius of 4.22 x 10⁸ m. From these data, determine the mass of Jupiter. Assume m_Io << m_Jupiter.

ans: 1.90 x 10²⁷ kg

Sec. 13 - Heat

Read: Ch. 18, sec. 4; Ch. 19, start - sec. 3 & sec. 6.

A. One liter of water at 30°C is used to make iced tea. How much ice at 0°C must be added to lower the temperature of the tea to 10°C?

ans: 223 g

B. 1. (3 points) A Thermos bottle consists of one glass bottle within another, with the air pumped out of the space between them. The glass walls are silvered like a mirror.

a. What type(s) of heat flow are inhibited by removing the air?

b. What type(s) of heat flow are inhibited by silvering the walls?

2. (7) A bar of gold is in thermal contact with a bar of silver of the same length and cross-section, as shown. Assuming steady state heat flow with no losses to the surroundings, what is the temperature of the junction between the metals?

ans: 51.2°C

C. 1. (2 pts) Why can you get a more severe burn from steam at 100°C than from water at 100°C?

2. (8) A 1.50 kg iron horseshoe initially at 600°C is dropped into 20.0 kg of water at 25.0°C. What is the final equilibrium temperature? (Neglect heat lost to the container or to vaporization of the water.)

ans: 29.6°C

D. A steel ball bearing is 4.000 cm in diameter at 20.0°C. A bronze plate has a hole in it that is 3.994 cm in diameter at 20°C. What common temperature must they have for the ball to just squeeze through the hole?

ans: 208°C

E. 1. (2 points) The specific heat of water is about two times that of ethyl alcohol. Equal masses of alcohol and water in separate beakers are supplied with the same amount of energy. Compare their temperature increases.

2. (8) A 3.00 g lead bullet at 30.0°C is fired at a speed of 240 m/s into a block of ice at 0°C, in which it becomes embedded. As a result, the ice becomes a mixture of ice and water. When thermal equilibrium is reached, what quantity of ice has melted?

ans: .294 g

F. 1. (2 points) You can hold the end of a glass rod whose other end is in a flame for a much longer time before burning your fingers than you can with a metal rod the same size. Explain why.

2. (8) The sun’s surface has a temperature of about 5800 K. Its radius is 6.96 x 10⁸ m. Assuming that it behaves like a blackbody, calculate the total energy radiated by the sun each day.

ans: 3.38 x 10³¹ J

Sec. 14: Fluid Mechanics

Read: Ch. 14: sec. 1 – 6 & 8.

A. The water supply enters a building at a pressure of 300 kPa, moving at .400 m/s through a pipe with a cross sectional area of 75.0 cm². All of this water flows through a 10.0 cm² pipe on the top floor, 25.0 m higher. (Only one faucet in the whole building is being used at the moment.) Find (a) the flow velocity and (b) the pressure in this top floor pipe.

ans: 3.00 m/s, 50.6 kPa

B. 1. (2 points) A person in a boat floating in a small pond throws a heavy anchor overboard. Does the level of the pond rise, fall, or remain the same?

2. (8) A small girl at a fair has a balloon filled with .0058 cubic meters of helium. The total mass of balloon plus helium is 3.15 grams. If she lets go of it, what will its upward acceleration be?

ans: 13.5 m/s²

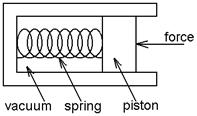
C. The spring of the pressure gauge shown in this cross-sectional view has a force constant of 1000 N/m, and the piston has a diameter of 2.00 cm. Find the depth in water for which the spring is compressed .500 cm more than it is at the surface.

ans: 1.62 m

D. 1. (2 points) Lead is denser than iron. If submerged in some fluid, is the buoyant force on a lead object greater than, less than, or equal to the buoyant force on a (lighter) iron object of the same volume?

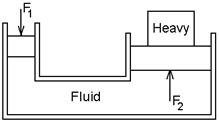2. (8) The small piston of a hydraulic lift has a radius of 1.00 cm, and its large piston has a radius of 8.00 cm. What force must be applied to the small piston for it to raise a load of 15.0 kN? (In service stations, this force is usually generated using compressed air.)

ans: 234 N

E. A plastic sphere floats in water with 50.0% of its volume submerged. This same sphere floats in glycerin with 40.0% of its volume submerged. Determine (a) the density of the glycerin and (b) the density of the sphere.

ans: 1250 kg/m³, 500 kg/m³

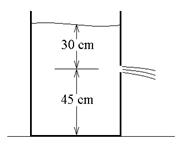
F. An open barrel full of water has a hole in it 30 cm below the water level and 45 cm above the ground.

a. With what speed does water shoot out of the hole? (Hint: The pressure is atmospheric at both the top surface of the water and at the hole.)

b. How far from the bottom of the barrel does the water hit the ground? (Think of the water as a stream of projectiles.)

ans: 2.42 m/s, .733 m