Experiment 9: Conservation of Angular Momentum

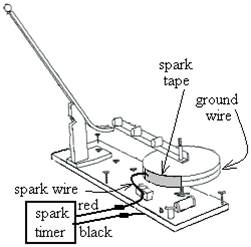
You will see if the angular velocity given to a turntable by a collision matches what is predicted by theory. A wooden disk is mounted on a vertical axle. An arm on the disk has a rubber cup at its end. A steel ball rolls down a ramp, then shoots into this cup, sticking there. The impact makes the system start to turn. The velocity of the wheel’s edge is found from dots left on it by a spark timer. The angular velocity is found from this and compared to what theory predicts.

Procedure.

Don't take the time to find uncertainties; just assume the final results are good to + 10%.

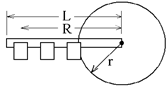The masses of the disk and arm (including the cups) are given on the answer sheet, to avoid disassembling the apparatus to measure them. Measure the mass of the ball m _ball, the radius of the disk r, the radius from the axis to the center of the ball when in the outermost cup R and the length from the axis to the end of the arm L.

Calculate the moment of inertia the system has when the ball is in the cup. (From their masses and dimensions, you can find I for each part and add them.) It is reasonably accurate to call the arm a “thin rod” even though there are concentrations of mass at the cups.

Put the apparatus at the edge of the counter where, with the arm turned away, a ball coming off the ramp will fly out over the floor. Level the apparatus by turning the three screws that support its base: If the disk stays at rest when released from any position, consider it level. If it turns by itself, raise the side where it ends up or lower the opposite side.

Find v_ball, the speed with which the ball leaves the ramp, using the same method as in the linear momentum lab: Place a piece of cardboard on the floor, centered a little over a meter beyond the end of the ramp. (These balls are heavier than in the momentum lab, and dent the floor without the cardboard for protection.) Also put some kind of backstop, such as a box, just beyond the impact site to stop the ball. Put a sheet of paper over carbon paper on the cardboard to record where the ball lands. Release the ball from the top of the ramp and let it fly across the room. Do a few trials to be sure you have the right spot. Then measure the vertical and horizontal distances which the bottom of the ball moves between the end of the ramp and this point on the floor. From the vertical distance, calculate the time the ball was in the air. The horizontal distance then gives you v, the speed with which it was launched.

Move the arm so the cup is at the end of the ramp. Check that the ground wire runs around the disk about halfway between the bottom and the top. Using scotch tape, attach about a foot of spark tape to the edge of the disk, preferably light side out, starting a little beyond the spark wire and going in the proper direction for the sparks to leave marks after the collision. Attach the spark timer to the apparatus, black to ground and red to the spark wire. Adjust the spark gap to just a millimeter or two, making sure the wire does not rub against the tape anywhere.

Caution: Do not use the spark timer without someone else in the room to pull the plug if you are being shocked. (The shock is capable of contracting the muscles in your hand so you can’t release what is shocking you.) Have the instructor approve your setup before you use it.

Set the timer for 10 sparks per second. Fire the sparks for a moment to be sure everything is working. With the cup still at the end of the ramp, release the ball and start the sparks. Stop them when the end of the tape goes by the spark wire. Turn the spark unit off, so the light on it goes out. If you need to get the ball back out of the cup, poke an unbent paperclip through the hole in the end.

The wheel gradually loses speed as it turns, so you want to use just the first few spark intervals after the collision to find the speed of the disk’s edge. Measure distance off the spark tape; get the corresponding time from knowing each spark interval is one tenth of a second. Be aware that the dots should be fairly evenly spaced; some may not have printed.

From this speed and the disk’s radius, find the “observed” angular velocity. Assume + 10%.

You now know the following conservation laws:

Energy: In the absence of nonconservative forces, a system's mechanical energy (kinetic plus potential) is conserved.

Linear Momentum: In the absence of external forces, a system's momentum is conserved.

Angular Momentum: In the absence of external torques, a system's angular momentum is conserved.

One of these things is conserved during this collision. State which one (the title of the lab is sort of a hint), and explain why by answering the following questions:

1. During the collision, there are friction forces between the ball and cup as the ball slides in. Are these forces conservative?

2. During the collision, is there a force on the ball-arm-disk system from outside the system? If so, what is it? (Hint: Imagine a ball hitting one end of a stick which is floating in water. The impact would make the stick start to rotate and drift across the water. But your apparatus only rotates, so something holds it back. Where on the disk or arm does the restraining force act?)

3. Does the external force you just identified produce any torque? (If not, why not?)

Use this conservation law to find the theoretical angular velocity of the wheel. Assume it is also 10% uncertain. Does it agree with the observed w?

PHY 131 Experiment 9: Conservation of Angular Momentum

m _disk = 726 g m _ball = m _arm = 159 g

r = R = L =

Find I:

Find v_ball:

Vertical distance = Horizontal distance =

Calculate t:

Calculate v_ball:

Spark tape: Distance = _______________ Time = ______________

Calculate speed:

Find observed w:

Answer Questions:

Calculate theoretical w: