Experiment 1B: Free Fall

PURPOSE: Measure the acceleration due to gravity.

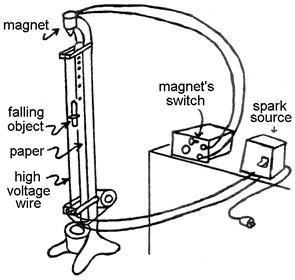
APPARATUS: An object suspended from an electromagnet falls when the magnet is turned off. There is a wire on each side of it as it falls. Every sixtieth of a second, a high voltage pulse is sent to one wire, making a spark jump to a metal ring on the falling object and from there to the other wire. The spark marks heat sensitive paper covering this second wire, periodically recording the object’s position.

CAUTIONS:

Do not use the apparatus without someone else in the room to pull the plug if you are being shocked.

The spark source's red lead should go to the free fall device's high voltage wire. The black (ground) lead goes to the connector at the right. Do not mix them up.

Do not move the apparatus or you may throw it out of level, making the object land improperly.

PROCEDURE.

1. When your group's turn comes, run off a tape:

a. Turn on the electromagnet with the key on its power supply.

b. Suspend the object from the electromagnet and steady it so that it hangs motionless.

c. Turn on the switch on the face of the spark source, which should be set for 60 Hz. Pick up the hand pushbutton and hold it down to turn on the sparks.

d. Switch off the power supply to drop the object. When it lands, take your thumb off the button and turn off the switch on the face of the spark source.

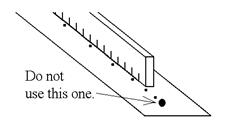
2. Lay your group’s tape on your table. Do not use the large first dot. Number the next fifteen dots after that. Time, in the answer sheet’s first column, is the dot number over 60 because there were 60 sparks per second. Stop when the table is full; there are more dots than you need.

Each interval should be just a little larger than the one before. If a dot is missing, ask what to do.

3. Put a meter stick on its edge so that its markings are right next to the dots. Record where the dots are. (Their position on an x axis along the tape, not the distance from the previous dot.) Magnifying glasses are available. Do not throw out the tape until you are told nothing needs rechecking.

4. In the third column, leave the first line blank because there is no line above it to subtract from. Also leave the last line blank because it has no line below it. On the rest, calculate Δx for the 2/60 second centered on that line’s dot. That is, Δx from the dot on the line above to the dot on the line below. Imitate this example:

Time, t (sec)	Position, x (cm)	Δx from dot before this one to dot after it (Δt = 1/30 s) Δx (cm)	Velocity, v = Δx/Δt (cm/s)
0	0.00	(leave blank)	(leave blank)
1/60	0.95	2.55	76.5
2/60	2.55	3.85	115.5
3/60	4.80	(leave blank)	(leave blank)

5. Keep in mind: Δx/Δt gives the average velocity during the time Δt. This equals the instantaneous speed at the midpoint of that interval. The weight starts out going slower than average and ends up faster than average. Therefore, to get v at dot 1, use an interval centered on dot 1, such as from 0 to 2. For v at dot 2, use the interval from 1 to 3. And so on.

Calculate the speed at each dot, except the first and last, using a Δx and Δt centered on that dot. Don't round off excessively. Keep in mind that dividing by 1/30 is the same as multiplying by 30. Try punching up the numbers in the example to be sure you see how it was done.

6. Before doing the fifth and sixth columns, plot a graph of velocity versus time. Observe these rules, as you should with any graph:

- Time goes on the horizontal axis.

- Pick a scale which makes the graph pretty much fill the page (without going off the edge.) A larger scale is more accurate.

- Label both axes with the variable plotted along each and the unit each is measured in.

7. Draw what appears to be a best fit line through your data: One that passes as close as possible to as many points as possible. (Computers will do the graphs for many of our labs, and they will do steps 6 through 10 for you. You're doing it by hand today so you know what the computer is doing. We are cutting a corner; you're just eyeballing the best fit line instead of calculating it like the computer does.)

8. Determine the probable error in the velocity data. (In lab 1A, you just estimated the uncertainties. This is a more rigorous approach based on how much the data varies.)

a. From the graph, read the deviation of each point from the best fit line, and record it in the fifth column of the table: This means the vertical distance from the point to the best fit line, as shown in this example.

b. In the last column, square each deviation. Find the total of these squared deviations.

c. Divide Σ (dev.)² by the number of points on the graph to get the average squared deviation, σ². Show how you set this up in the space between the equal signs. The square root of this is called "standard deviation," usually represented by the letter σ.

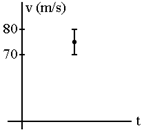9. So, σ is the uncertainty in v. When an uncertain number is plotted on a graph, the uncertainty is indicated using an “error bar.” This means to draw a line through the whole possible range rather than just a dot at the best value. The "true" value could lie anywhere on the error bar. For example, if 75 + 5 cm/s was one of your data points (5 cm/s being σ), you would draw an error bar from 70 cm/s to 80 cm/s. The uncertainty in the time is small enough to ignore, but if it was not, there would also be a horizontal error bar.

Include the error bars on your graph. Since σ is just the range which the experimental errors are probably in, the best fit line might miss a few of the error bars, but it should pass through most of them, and not miss the rest by much.

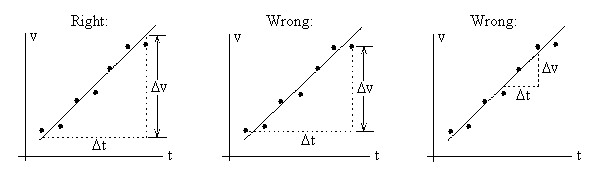
10. Find the slope of your graph to obtain the object’s acceleration. Observe the following rules which, again, also apply to all future labs:

- Find it from the best fit line, as in the picture on the left, not from points which lie off the line as in the middle. (The line averages out some of the random errors in individual points.)

- Find it from points near opposite ends of the line, not points near each other as on the right. (If small numbers are off a little, it makes more difference than if big numbers are off a little.)

Show all steps of the calculation, including uncertainties with each step, as usual. Use the rules from last week's lab. For the uncertainty in Δt, the manufacturer claims that the spark timer is accurate to +1%.

Example: Let's say σ came out 5 cm/s, and that you are finding the slope between the points (2/60 s, 100 cm/s) and (14/60 s, 360 cm/s):

a = v_f - v_i = (360 ± 5) - (100 ± 5) = 260 ± 10 = 260 ± 3.8%

t_f - t_i (14/60 - 2/60) ± 1% 12/60 ± 1% .2 ± 1%

= 1300 ± 4.8% = 1300 ± 62 cm/s² ans.

(You probably won't get exactly the accepted value. You have to figure out the uncertainty so you know if you came close enough to say the lab worked.)

Conclusion: Within your uncertainty, does your value for g agree with the accepted one? (Since the uncertainty is the range your error is probably in, there is a small chance you could land just outside.)

PHY 131 Experiment 1B – Free Fall

DATA TABLE:

Time, t (sec)	Position, x (cm)	Δx from dot before this one to dot after it (Δt = 1/30 s) Δx (cm)	Velocity, vx =Δx/Δt (cm/s)	deviation (cm/s)	(dev.)^2 (cm^2/s^2)
		(leave blank)	(leave blank)	(leave blank)	(leave blank)
		(leave blank)	(leave blank)	(leave blank)	(leave blank)

Σ (dev.)² = ___________

Attach graph, calculate g below. σ² = = ___________

σ = ___________