Experiment 1A: Measurement and Error

In most of our labs, you measure something then compare to what is predicted by theory. These numbers are seldom equal, because measurement is never exact. Today, we look at the rules for deciding how close is close enough; whether the difference is just what you should have expected.

Measurements can be affected by several kinds of errors. One kind is mistakes. Another is systematic errors, due to some kind of bias in the measurements. Then there are errors due to experimental uncertainty, the fact that no method of measuring is accurate to an infinite number of decimal places. These errors tend to be random, so they can be analyzed statistically, but unlike other kinds of errors, they cannot be eliminated by being careful. Therefore, measurement does not give you a precise value, but simply a range of possibilities. Notation: 4.73+.01 cm means that you've reasonably sure the true value lies between 4.72 cm and 4.74 cm. (You don't know where between 4.72 and 4.74 the exact number lies; 4.73 is just the middle of that range. A best guess.)

If you do a calculation using uncertain numbers, the result is also uncertain:

- If adding or subtracting the measurements, add the uncertainties. (In the same units

as the best value, not as percents.)

- If multiplying or dividing, convert the uncertainties to percents, then add the percents.

PERCENTS: You will probably want to refer to this during future labs, so remember it is here:

To find what one number is as a percentage of another, divide (and multiply by 100):

Example: 3.5 + .2 cm (.2 / 3.5) x 100% = .057 x 100% = 5.7%

3.5 cm + 5.7%

To find some percentage of a number, multiply:

Example: 3.5 cm + 5.7% 5.7% of 3.5 cm = (.057)(3.5 cm) = .2 cm

3.5 + .2 cm

Part 1: Volume of a Solid Cylinder.

You will check whether the formula V= πr²h gives the correct volume for a solid plastic cylinder.

1. With a ruler, measure its diameter and height, estimating uncertainty. (While measuring, say to yourself “I’m sure it’s less than this and more than that.”) Calculate the volume from the formula.

2. Determine the volume’s uncertainty with the rules given above. Imitating this example will help.

Example: Find the volume of a cylinder of diameter 1.80 + .05 cm and height 2.50 + .05 cm.

x 100% = 2.8%

Answer: r = ½ d = (.5 + 0%)(1.80 + 2.8%) = .90 + (0 + 2.8)% = .90 cm + 2.8%

The ½ is not a measured number, so it is not uncertain.

Notice the radius has the same percent uncertainty as the diameter, not the same number of cm.

V= πr²h = (3.14 … + 0%)(.90 + 2.8%)(.90 + 2.8%)(2.50 + 2.0%)

= 6.3617 … + (0 + 2.8 + 2.8 + 2.0)%

= 6.3617 … + 7.6%

7.6% of 6.3617 = (.076)(6.3617) = .4835 Rounding, V = 6.4 + .5 cm³

Notice that because r is squared, its percent uncertainty is counted twice.

The answer is rounded to the nearest tenth because the last significant figure is the one which is somewhat, but not completely, uncertain. With an uncertainty of a few tenths, we have some vague information at that level. We have no idea what goes in the hundredths place.

3. Put some water in a 100 ml graduated cylinder and record its volume, estimating an uncertainty. Add the solid cylinder and record the total volume of water plus cylinder. Subtract to get the volume of the solid cylinder, using the rule from the previous page to get the uncertainty.

4. In your conclusion, state whether the volume measured by displacing water agrees with the volume calculated by the formula. That is, do the two ranges of possible values have some common ground? For example, 3.0 + .2 agrees with 3.21+.02, but 3.0 + .1 does not agree with 3.21+.02.

Part 2: Volume of a metal block.

You will repeatedly measure the volume of a metal block, using a more accurate instrument each time. The values you get for the volume should all agree with each other, within their uncertainties.

From the set of five blocks, select one. You will not use the others. (Do not put it in water.)

a. Ruler. Measure the block’s length, width and height with a ruler. If the 0 mark isn't clear, you may find it's better to put the edge of the block at the 1 cm mark, then subtract 1 cm from the reading. Read the ruler as accurately as possible, estimating tenths of a millimeter. Estimate a reasonable uncertainty for each measurement. Calculate a best value for V. Use the rules in the box to find V's uncertainty. Remember to include units on all values.

b. Vernier Caliper. (See diagram, next page.) To read a vernier caliper:

a. Read how many whole millimeters you have from the main scale.

b. Read tenths of a millimeter from the vernier scale by looking for which mark best lines up with one on the main scale. A magnifying glass is available, if it would help you see the marks.

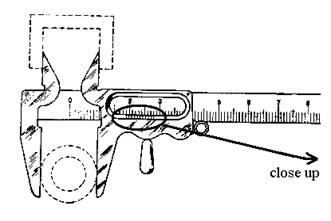
Measure the block’s dimensions, reading the instrument as accurately as possible, and estimate the uncertainty. Calculate V and its uncertainty.

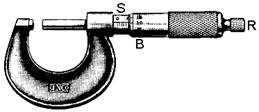c. Micrometer.

The screw inside has a half-millimeter thread, so one turn advances the jaw and also the barrel B, .5 mm. The barrel has 50 marks around it, so turning it by one division moves the jaw .01 mm.

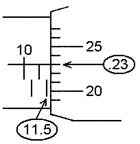Tighten the jaws onto the object to be measured until the ratchet, R, slips. Do not force it farther. Add the reading from the main scale to the reading from the barrel. In this example, 11.5 mm from the main scale is added to .23 mm from the barrel, making the reading 11.73 mm (or 1.173 cm).

Check that your micrometer is correctly zeroed (they get out of adjustment fairly easily) then measure the two smaller dimensions of the block.

The micrometer does not open wide enough to measure its largest dimension; re-use your value from the vernier caliper. Once again calculate V with its uncertainty.

As your conclusion, answer the following:

- Does V from the vernier caliper agree with V from the ruler?

- Does V from the micrometer agree with V from the ruler?

- Does V from the micrometer agree with V from the vernier caliper?

If your V's do not agree, you've made a mistake. Find and correct it. One possibility is that your estimated uncertainties might not have been very good estimates.

Notice that the increasing accuracy of the instruments only reduces, does not eliminate, experimental errors. Any number based on measurement has at least a small range of uncertainty.

PHY 121 Experiment 1A: Measurement & Error

Reminders:

1. Hand labs in before leaving unless I sign them.

2. Work in pencil (or work out mistakes on a first draft.)

3. Write a discussion of the experiment (Objective/Procedure/Conclusion) to hand in with this answer sheet. Don't forget to put your name on it.

Part 1:

diameter = __________ + __________ height = __________ + ___________

Show calculation of V and its cm³ of uncertainty:

Grad. cylinder: V of water = _________ + ________ V water + cyl. = __________ + _________

V of cylinder & its uncertainty:

Part 2:

a. Ruler: Dimensions: _________ + _______, _________ + _______, _________ + _______

Calculate V and uncertainty:

b. Vernier Caliper: _________ + _______, _________ + _______, _________ + _______

Calculate V and uncertainty:

Use the back for (c) Micrometer.