PHY 100 ASSIGNMENT 7

1. Zero. (The waves are exactly out of step with each other, so they cancel.)

2. Two. (I'll bet you said four, didn't you?) The rope would hold four node to node segments, each of which is half a wavelength.

3. This makes the string heavier, so waves travel along it slower, which lowers the frequency. (By f = v/λ, a lower speed means a lower frequency.)

4. a. A node is a point of minimum vibration.

b. An antinode is a point of maximum vibration.

5. They sound the instrument and some reference tone, like a tuning fork, at the same time. As they adjust the instrument closer to the reference tone, the beats get slower; when they match, the beats stop.

6. If their marching happened to be at one of the bridge's resonant frequencies, the standing waves they set up could shake the bridge apart. (Soldiers have been given this order since 1831, when this happened to a suspension bridge near Manchester, England.)

7. The diagram shows the pattern of vibration that goes with the fundamental frequency. Notice that N to N = 60 cm. λ is twice the node to node distance, so λ = 120 cm.

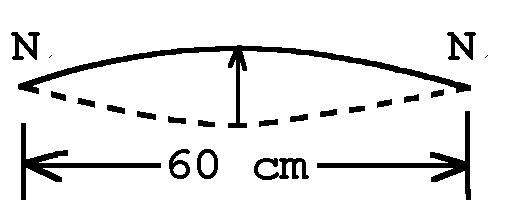
8. f = v/λ = (12 m/s)/(1.2 m) = 10 Hz (Notice 120 cm must be converted to 1.2 m to be consistent with the unit on v.)

9. The higher harmonics are whole number multiples of the fundamental:

a. 2 x 220 = 440 Hz

b. 3 x 220 = 660 Hz

10. C is just a pure sine wave, and so contains only the fundamental. A, B, and D are more complex shapes, which are made by adding in overtones.

11. Twice the amplitude of each individual wave. (Waves that are in step reinforce each other.)

12. It says on your formula sheet that sound in a tube has an antinode at an open end. So, draw those in. For the fundamental frequency, you want the wavelength as long as possible, so don’t put any other antinodes in between. Any pair of antinodes has a node halfway between, so draw that in. So, the answer looks like this.

13. λ = 2(A to A) = 2(.6 m) = 1.2 m

f = v/λ = (340 m/s)/(1.2 m) = 283 Hz

14. Each node to node segment of the standing wave is half a wavelength long. The number of these segments along the string equals the harmonic number.

a. second harmonic: two half-wavelength segments add up to one wavelength.

b. fourth harmonic: four half-wavelength segments make two wavelengths.

15. They differ in quality.

16. a. λ = 2(N to N), so N to N is 2.0 m because 4 = 2(2).

b. λ = 4(N to A), so N to A is 1.0 m.

17. The fourth harmonic is four times the fundamental. That makes the fundamental 600/4 = 150 Hz. The others are multiples of this fundamental. 150 x 2 = 300 Hz. 150 x 3 = 450 Hz.

18. a. A and C. Loudness corresponds to amplitude, and A is just as tall as C.

b. A and D. Pitch corresponds to the period (or frequency). If you measure horizontally along each graph, you'll find that one complete period has the same length on A as on D.

c. A and B. Quality corresponds to the shape of the wave ("waveform"). B, while smaller than A, has the same shape.

19. A standing wave.

20. Beats.

21. Loosened. He wants the beats to stop, so when he went from 3 to 5, he was going the wrong way.

22. a. Reduce the tension: This reduces the speed of the waves, which reduces the frequency by f = v/λ.

b. Make it heavier (thicker): This reduces the speed of the waves, which reduces the frequency by f = v/λ.

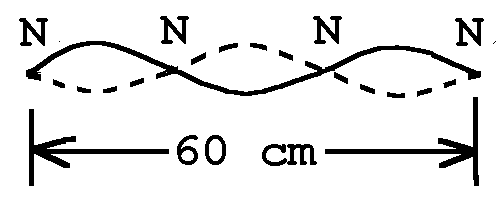
23. As shown, N to N is 20 cm. (60 cm divided into three equal pieces.) So, λ is 40 cm because it’s twice the distance between nodes.

24. Loudness.

25. Resonance.